Deze site is samen met de grote zuster op mrooijer.blogt al 4 keer gehackt. Alle wachtwoorden zijn in orde; ergens diep in de krochten van WordPress zit een veiligheidslek. Kan ik niet vinden en is ook mijn werk niet. Er zit niets anders op dan overnieuw beginnen met een simpele en werkende nieuwe lay-out en […]
Global Temperatures April 2016
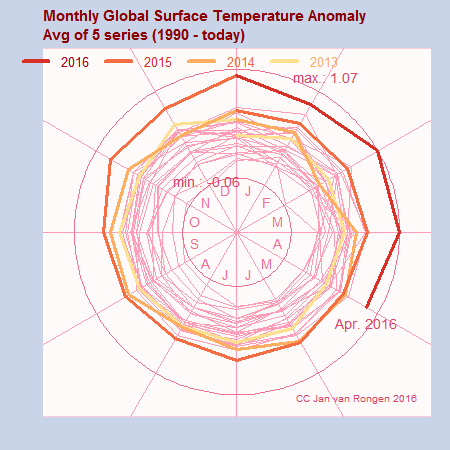
In the meantime showing a circular diagram has become popular. here is the avg of 5 series: HadCRUT4.4, GISS, NOAA, JMA and BEST. The 12th month that this average is a record month. It is going down a bit after the El Nino has stopped, but not by much. This is what can be expected from […]
Weg “pauze”
Ik leverde commentaar op een verouderde grafiek op de site van Crok. Hier de update van die grafiek De lijn is een ( op een wat speciale manier berekende) maat voor de temperatuurstijging in de periode van het aangegeven jaartal tot “heden”, in het geval van de gebruikte grafiek was dat 2012/8. Zoals je ziet […]
Warme lente en herst
N.a.v. wat recente uitspraken nog maar eens naar de maandgemiddelden van de temperaturen in De Bilt gekeken. Ja: gemiddelden van de gemiddelde dagtemperatuur. Het meest opvallende is dat ergens in de jaren 70-80 er een omslag is; zo schelen de gemiddelden voor en na 1980 meer dan een graad . Maart, april en november springen er […]
